R-4
In equation (8),
E
cell
o
is the cell potential under standard conditions, Q is the reaction quotient for the
overall cell reaction and n is the number of electrons exchanged in the cell reaction.
Alternately, we can treat the cell potential as the sum of two half-cell potentials. The two half-cell
potentials can be calculated using the Nernst equation for each of them and then substituted into
equation (7) to get the cell potential. We will consider each approach, (next page), in turn.
1. Method 1: Using the Overall Cell Reaction
In order to write a balanced chemical equation for the overall cell reaction, we must first balance the
number of electrons gained in the reduction process with the number of electrons lost in the oxidation
process. Thus, in this example we must multiply equation (3) by 2 and equation (5) by 5. The balanced
half-cell equations will be:
2 MnO
4
-
(aq)
+ 16 H
+
(aq)
+ 10 e
-
2 Mn
2+
(aq)
+ 8 H2O
(l)
5 Zn
2+
(aq)
+ 10 e
-
5 Zn
(s)
.
The overall cell reaction is obtained by adding the equation for the oxidation of Zn
(s)
to the equation for
the reduction of MnO
4
-
(aq)
:
2 MnO
4
-
(aq)
+ 16 H
+
(aq)
+ 5 Zn
(s)
2 Mn
2+
(aq)
+ 8 H2O
(l)
+ 5 Zn
2+
(aq)
(9)
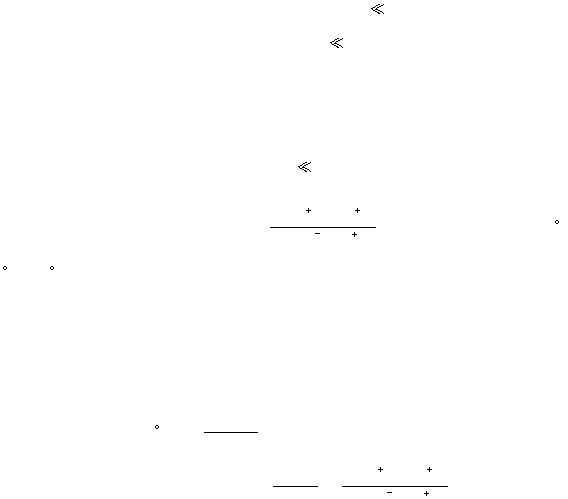
The reaction quotient, Q, for equation (9) is
[
]²
[
]
[
]²
[
]
Mn
Zn²
MnO
H
2
5
4
16
and n is 10. The value of E
cell
equals
E
red
+ E
ox
. Note that E° for a half-cell reaction is not changed even if the half-cell is multiplied
by an integer. Electrode potentials and cell potentials are intensive quantities like density. Density is
mass per unit volume, so values of density are independent of the volume of the sample. A volt is 1
joule of work per unit of charge transferred so values of E° are independent of the number of
charges or electrons transferred. Therefore:
E
cell
= E
cell
-
0.0592
n
log Q
cell
E
cell
= [1.50 V + (0.76 V)] -
0.
0592
10
log
[
]²
[
]
[
]²
[
]
Mn
Zn²
MnO
H
2
5
4
16
(10)