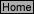R-2
E = E
-
0.
0592
n
log Q
(1)
When equation (1) is applied to a full cell, Q is the reaction quotient (as described in Experiment E and
in your text book), n represents the number of moles of electrons exchanged in a balanced redox
reaction, and E° is the difference between the two standard half-cell potentials. For a general redox
equation:
aA
(aq)
+ bB
(aq)
cC
(aq)
+ dD
(aq)
the reaction quotient, Q, is defined as:
b
a
d
c
B
A]
D
C
Q
]
[
[
]
[
]
[
(2)
where a, b, c and d are stoichiometric coefficients in the balanced equation.
The Nernst equation applies to the half-cells as well as to the full cell. In each half-cell, Q applies to the
half-cell reaction and E° is the standard half-cell potential. If the concentrations are all 1.00 M, then Q
= 1, log Q = 0, and E = E°. Note: if the concentrations are adjusted so that Q = 1 (even though the
concentrations of individual species may not be 1.00 M), E also equals E°.
Let us consider two examples. For the first example, let us consider the reduction of an extremely
strong oxidizing agent, potassium permanganate:
MnO
4
-
(aq)
+ 8 H
+
(aq)
+ 5 e
-
Mn
2+
(aq)
+ 4 H2O
(l)
(3)
for which n = 5 and E° = 1.51 V. The electrode potential represents the tendency for MnO
4
-
to be
reduced to Mn
2+
if all species in the half-cell are 1.00 M. If all concentrations are not 1.00 M, the half-
cell potential is not 1.51 V, and the Nernst equation is needed to obtain the half-cell potential. For
reaction (3):
Q =
[
]
[
][
]
Mn
MnO
H
2
4
8
so the Nernst equation is:
E (volts) = 1.51 -
0.0592
5
log
[
]
[
][
]
Mn
MnO
H
2
4
8
(4)
In a second example, the reduction of Zn occurs by:
Zn
2+
+ 2 e
-
Zn
(5)